Category: My Favorite Sequences
-

My Favorite Sequences: A263135
—
by
This is the fourth in my installment of My Favorite Sequences. This post discusses sequence A263135 which counts penny-to-penny connections among \(n\) pennies on the vertices of a hexagonal grid. I published this sequence in October 2015 when I was thinking about hexagonal-grid analogs to the “Not Equal” grid. The square-grid analog of this sequence…
-

My Favorite Sequences: “Not Equal” Grid
—
by
This is the third installment in a recurring series, My Favorite Sequences. This post discusses OEIS sequence A278299, a sequence that took over two years to compute enough terms to add to the OEIS with confidence that it was distinct. This sequence is discussed in Problem #23 of my Open Problems Collection, which asks for…
-

My Favorite Sequences: A289523
—
by
This the second post in a recurring series, My Favorite Sequences. If you like this sort of thing, check out the Integer Sequence Review from The Aperiodical! A289523: Packing Circles of Increasing Area In July 2017, I added a mathematically-silly-but-visually-fun sequence, A289523. The sequence works like this: place a circle of area \(\pi\) centered at…
-
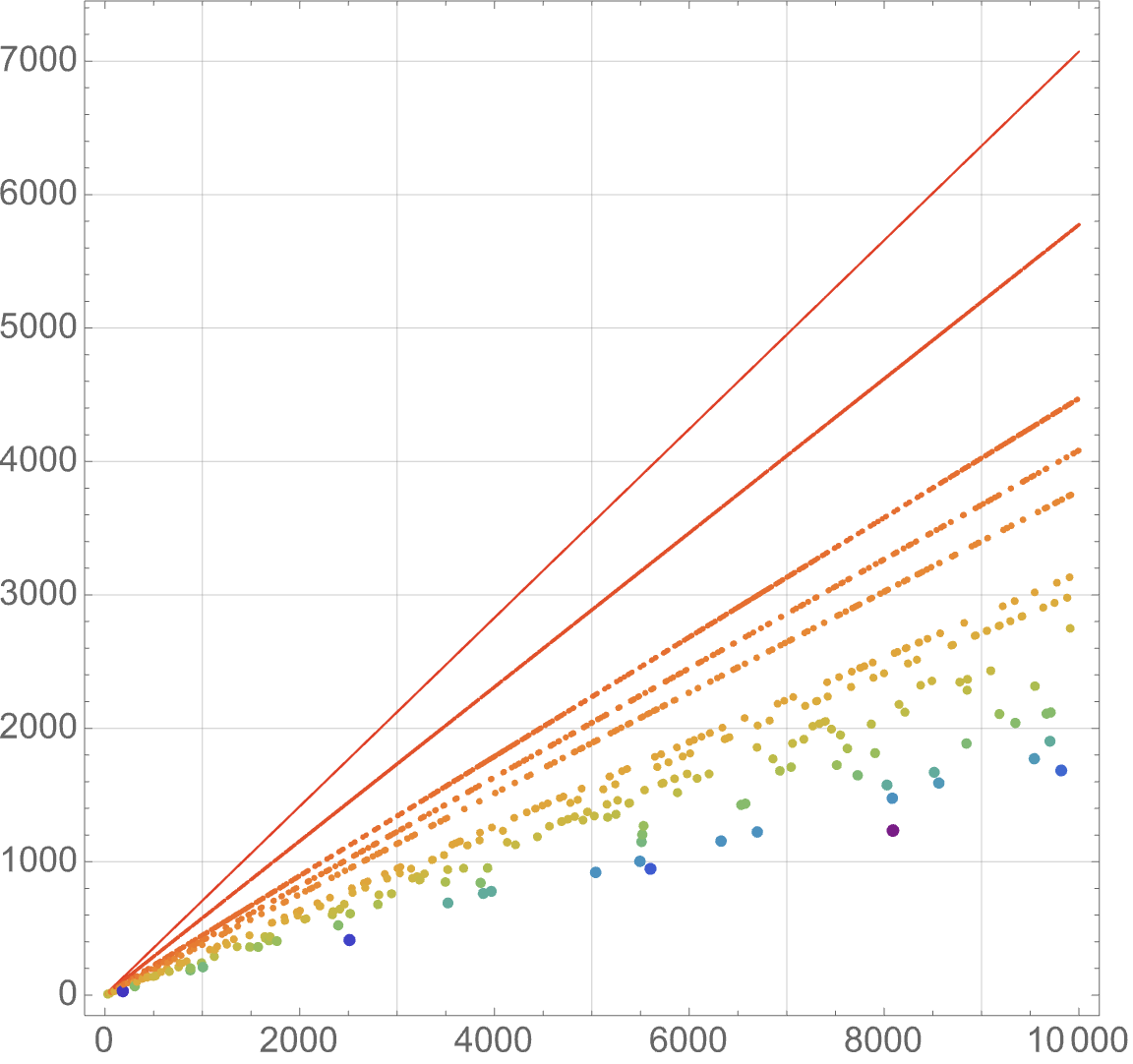
My Favorite Sequences: A261865
—
by
This is the first installment in a new series, “My Favorite Sequences”. In this series, I will write about sequences from the On-Line Encyclopedia of Integer Sequences that I’ve authored or spent a lot of time thinking about. I’ve been contributing to the On-Line Encyclopedia of Integer Sequences since I was an undergraduate. In December…