Regular Truchet Tilings

I recently made my first piece of math art for my apartment: a 30″×40″ canvas print based on putting Truchet tiles on the truncated trihexagonal tiling.

I first became interested in these sorts of patterns after my former colleague Shane sent me a YouTube video of the one-line Commodore 64 BASIC program:
10 PRINT CHR$(205.5+RND(1)); : GOTO 10

I implemented a version of this program on my website, with the added feature that you could click on a section to recolor the entire component, and this idea was also the basis of Problem 2 and Problem 31 in my Open Problem Collection.

I saw this idea generalized by Colin Beveridge in the article “Too good to be Truchet” in Chalkdust Magazine. In this article, Colin counts the ways of drawing hexagons, octagons, and decagons with curves connecting the midpoints of edges, and regions colored in an alternating fashion. In the case of the hexagon, there are three ways to do it, one of which looks like Palago tiles.

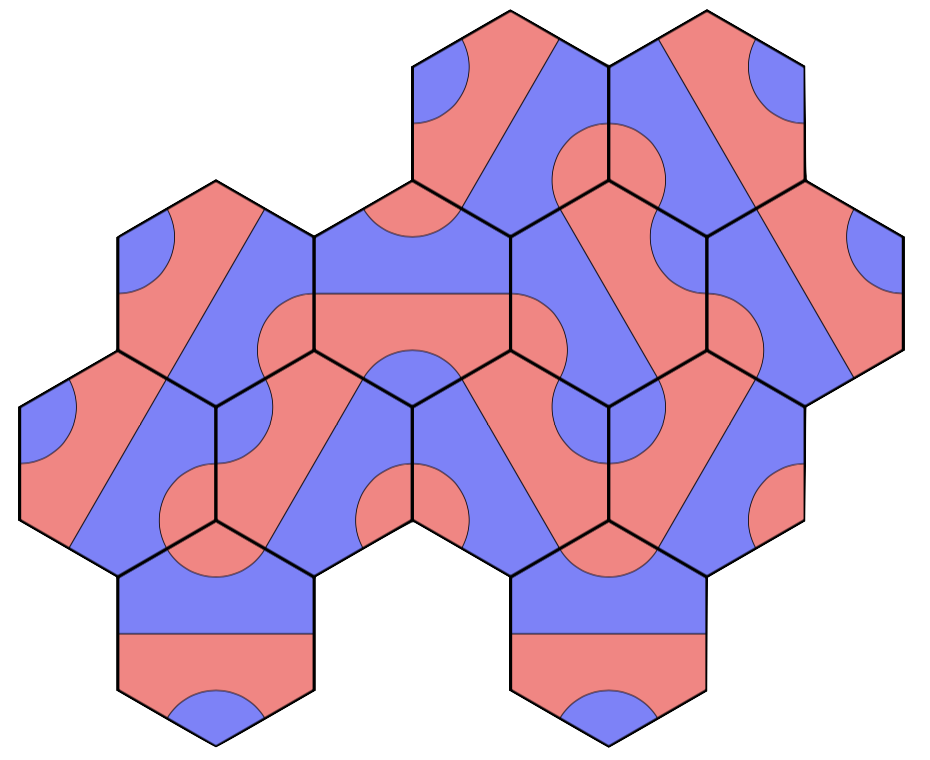
It turns out that if you ignore the colors, the number of ways to pair up midpoints of the sides of a \(2n\)-gon in such a way that the curves connecting the midpoints don’t overlap is given by the \(n\)-th Catalan number. For example, there are \(C_4 = 14\) ways of connecting midpoints of the sides of an octagon, where different rotations are considered distinct.

There are three regular tilings of the plane by \(2n\)-gons, the square tiling, the truncated square tiling, and the truncated trihexagonal tiling. Placing a Truchet tile uniformly at random over each of the \(2n\)-gons, results in a really lovely emergent structure.

If you find these designs as lovely as I do, I’d recommend taking a look at the Twitter bots @RandomTiling by Dave Richeson and @Truchet_Nested/@Trichet_Nested by @SerinDelaunay (based on a idea from Christopher Carlson) which feature a series of visually interesting generalizations of Truchet tilings and which are explained in Christopher’s blog post “Multi-scale Truchet Patterns“.

Edward Borlenghi has a blog post “The Curse of Truchet’s Tiles” about how he tried—mostly unsuccessfully—to sell products based on Truchet tiles, like carpet squares and refrigerator magnets (perhaps similar to “YoYo” magnets from Magnetic Poetry). The post is filled with lots of cool, alternative designs for square Truchet tiles and how they fit together. Edward got a patent for some of his ideas, and his attempt to sell these very cool products feels like it could have been my experience in another life.

If you want to see more pretty images and learn more about this, make sure to read Truchet Tilings Revisited by Robert J. Krawczyk! If you want to see what this looks like on a spherical geometry, check out Matt Zucker’s tweet. And if you want to try to draw some of these patterns for yourself, take a look at @Ayliean’s Truchet Tiles Zine.

📐The printable version of the Truchet Tiles Zine, for personal use or to sneak some Math into your loved one's lives https://t.co/C8MzRICDTE

🤓💗Join @becky_k_warren @nhoskee @Public_Math and I for the Math Zine Fest on 27th February: https://t.co/tTq6ikF7Gf pic.twitter.com/NnTcrwc7NS

— Ayliean (@Ayliean) February 7, 2021