This is the first installment in a new series, “My Favorite Sequences”. In this series, I will write about sequences from the On-Line Encyclopedia of Integer Sequences that I’ve authored or spent a lot of time thinking about.
I’ve been contributing to the On-Line Encyclopedia of Integer Sequences since I was an undergraduate. In December 2013, I submitted sequence A233421 based on problem A2 from the 2013 Putnam Exam—which is itself based on “Ron Graham’s Sequence” (A006255)—a surprising bijection from the natural numbers to the non-primes. As of today, I’ve authored over 475 sequences based on puzzles that I’ve heard about and problems that I’ve dreamed up.
A261865: Multiples of square roots
(This problem is closely related to Problem 13 in my Open Problems Collection.)
In September 2015, I submitted sequence A261865:
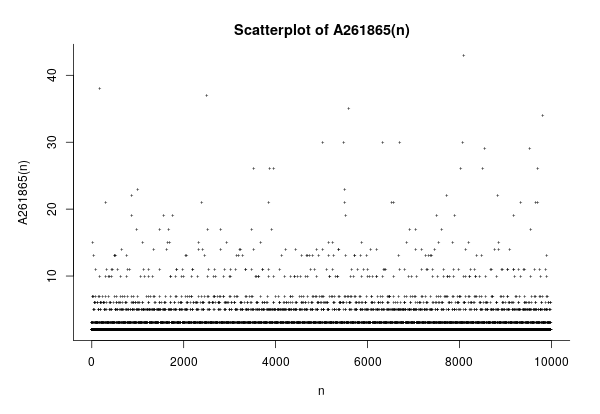
\(A261865(n)\) is the least integer \(k\) such that some multiple of \(\sqrt k\) falls in the interval \((n, n+1)\).

For example, \(A261865(3) = 3\) because there is no multiple of \(\sqrt 1\) in \((3,4)\) (since \(3 \sqrt{1} \leq 3\) and \(4 \sqrt{1} \geq 4\)); there is no multiple of \(\sqrt{2}\) in \((3,4)\) (since \(2 \sqrt{2} \leq 3\) and \(3 \sqrt 2 \geq 4\)); but there is a multiple of \(\sqrt 3\) in \((3,4)\), namely \(2\sqrt 3\).
As indicated in the picture, the sequence begins $$\color{blue}{ 2,2,3,2,2},\color{red}{3},\color{blue}{2,2,2},\color{red}{3},\color{blue}{2,2},\color{red}{3},\color{blue}{2,2,2},\color{red}{3},\color{blue}{2,2},\color{red}{3},\color{blue}{2,2},\color{magenta}{7},\dots.$$
A conjecture about density
As the example illustrates, \(1\) does not appear in the sequence. And almost by definition, asymptotically \(1/\sqrt 2\) of the values are \(2\)s.
Let’s denote the asymptotic density of terms that are equal to \(n\) by \(d_n\). It’s easy to check that \(d_1 = 0\), (because multiples of \(\sqrt 1\) are never between any integers) and \(d_2 = 1/\sqrt 2\), because multiples of \(\sqrt 2\) are always inserted. I conjecture in Problem 13 of my Open Problem Collection that $$a_n = \begin{cases}\displaystyle\frac{1}{\sqrt n}\left(1 – \sum_{i=1}^{n-1} a_i\right) & n \text{ is squarefree}\\[5mm] 0 & \text{otherwise}\end{cases}$$
If this conjecture is true, then the following table gives approximate densities.
| \(i\) | \(d_i\) |
|---|---|
| \(1\) | \(d_1 = 0\%\) |
| \(2\) | \(d_2 = 70.7\%\) |
| \(3\) | \(d_3 = 16.9\%\) |
| \(4\) | \(d_4 = 0\%\) |
| \(5\) | \(d_5 = 5.54\%\) |
| \(6\) | \(d_6 = 2.79\%\) |
| \(7\) | \(d_7 = 1.53\%\) |
| \(10\) | \(d_{10} = 0.797\%\) |
| \(11\) | \(d_{11} = 0.519\% \) |
| \(399\) | \(d_{399} = 3.53 \times 10^{-11} \%\) |
This was computed with the Mathematica code:
d[i_] := (d[i] = If[
SquareFreeQ[i],
N[(1 - Sum[d[j], {j, 2, i - 1}])/Sqrt[i], 50],
0
])
Finding Large Values
I’m interested in values of \(n\) such that \(A261865(n)\) is large, and I reckon that there are clever ways to construct these, perhaps by looking at some Diophantine approximations of \(\sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{6}, \dots\). In February, I posted a challenge on Code Golf Stack Exchange to have folks compete in writing programs that can quickly find large values of \(A261865(n)\).
Impressively, Noodle9’s C++ program won the challenge. In under a minute, this program found that the input \(n=1001313673399\) makes \(A261865\) particularly large: \(A261865(1001313673399) = 399\). Within the time limit, no other programs could find a value of \(n\) that makes \(A261865(n)\) larger.
| \(n\) | Order of magnitude | \(A261865(n)\) | Time |
|---|---|---|---|
| 1 | \(1 \times 10^{0}\) | 2 | (0s) |
| 3 | \(3 \times 10^{0}\) | 3 | (0s) |
| 23 | \(2.3 \times 10^{1}\) | 7 | (0s) |
| 30 | \(3.0 \times 10^{1}\) | 15 | (0s) |
| 184 | \(1.84 \times 10^{2}\) | 38 | (0s) |
| 8091 | \(8.091 \times 10^{3}\) | 43 | (0s) |
| 16060 | \(1.606 \times 10^{4}\) | 46 | (0s) |
| 16907 | \(1.691 \times 10^{4}\) | 58 | (0s) |
| 20993 | \(2.099 \times 10^{4}\) | 61 | (0s) |
| 26286 | \(2.629 \times 10^{4}\) | 97 | (0s) |
| 130375 | \(1.304 \times 10^{5}\) | 118 | (0s) |
| 169819 | \(1.698 \times 10^{5}\) | 127 | (0s) |
| 2135662 | \(2.136 \times 10^{6}\) | 130 | (0s) |
| 2345213 | \(2.345 \times 10^{6}\) | 187 | (0s) |
| 46272966 | \(4.627 \times 10^{7}\) | 193 | (1s) |
| 222125822 | \(2.221 \times 10^{8}\) | 210 | (5.2s) |
| 237941698 | \(2.379 \times 10^{8}\) | 217 | (5.7s) |
| 257240414 | \(2.572 \times 10^{8}\) | 227 | (6.2s) |
| 1205703469 | \(1.206 \times 10^{9}\) | 267 | (31s) |
| 1558293414 | \(1.558 \times 10^{9}\) | 299 | (41.8s) |
| 4641799364 | \(4.642 \times 10^{9}\) | 303 | (2.1m) |
| 6600656102 | \(6.601 \times 10^{9}\) | 323 | (3m) |
| 11145613453 | \(1.115 \times 10^{10}\) | 335 | (5.2m) |
| 20641456345 | \(2.064 \times 10^{10}\) | 354 | (9.8m) |
| 47964301877 | \(4.796 \times 10^{10}\) | 358 | (22.9m) |
| 105991039757 | \(1.06 \times 10^{11}\) | 385 | (52m) |
| 119034690206 | \(1.19 \times 10^{11}\) | 397 | (59.1m) |
| 734197670865 | \(7.342 \times 10^{11}\) | 455 | (6.4h) |
| 931392113477 | \(9.314 \times 10^{11}\) | 501 | (8.4h) |
| 1560674332481 | \(1.561 \times 10^{12}\) | 505 | (14.2h) |
Related Ideas
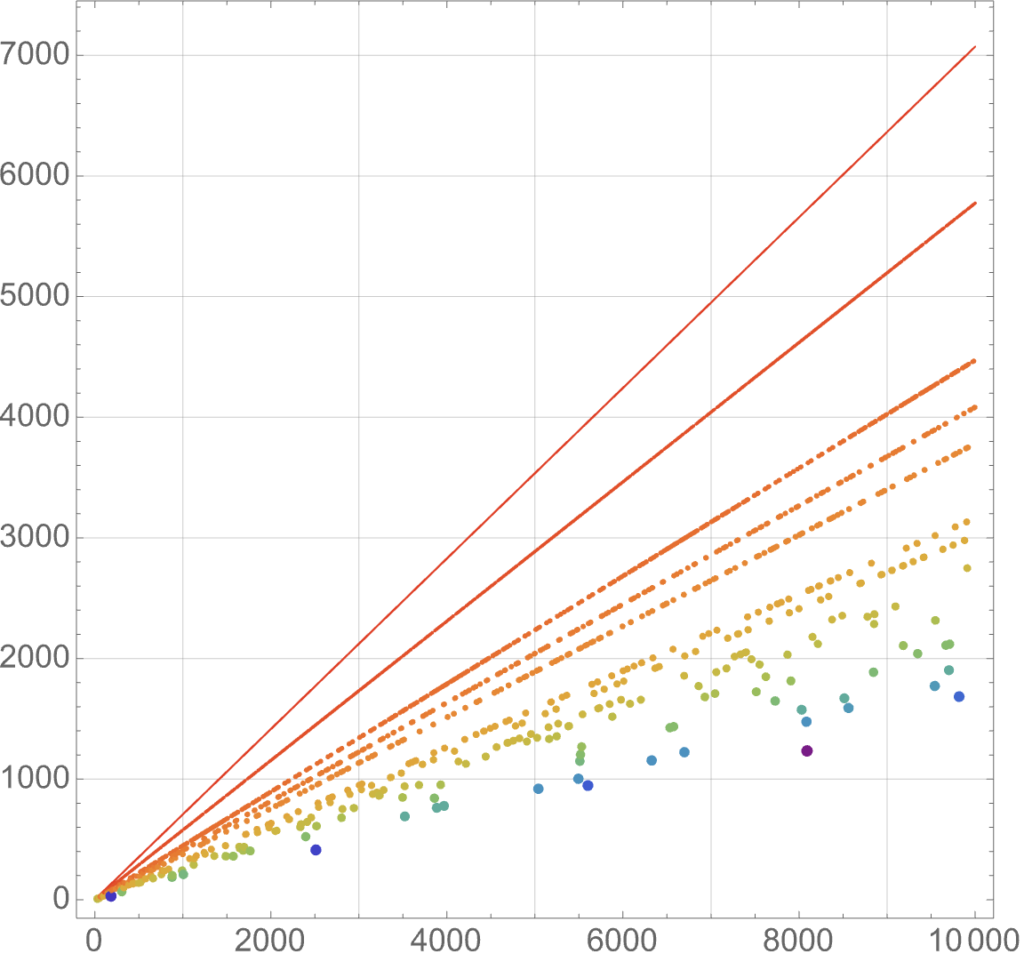
Sequence \(A327953(n)\) counts the number of positive integers \(k\) such that there is some integer \(\alpha^{(n)}_k > 2\) where \(\alpha^{(n)}_k\sqrt{k} \in (n, n+1)\). It appears to grow roughly linearly like \(A327953(n) \sim 1.3n\), but I don’t know how to prove this.
- Take any function \(f\colon\mathbb N \rightarrow \mathbb R\) that is positive, has positive first derivative, and has negative second derivative. Then, what is the least \(k\) such that some multiple of \(f(k)\) is in \((n,n+1)\)?
- For example, what is the least integer \(k \geq 3\) such that there is a multiple of \(\ln(k)\) in \((n, n+1)\)?
- What is the least \(k \in \mathbb N\) such that there exists \(m \in \mathbb N\) with \(k2^{1/m} \in (n,n+1)\)?
- What is the least \(m \in \mathbb N\) such that there exists \(k \in \mathbb N\) with \(k2^{1/m} \in (n,n+1)\)?
- A343205 is the auxiliary sequence that gives the value \(m\) such that \(m\sqrt{A261865(n)} \in (n, n+1)\). Does this sequence have an infinite limit inferior?
If you can answer any of these questions, or if you spend time thinking about this, please let me know on Twitter, @PeterKagey!
Leave a Reply