Tag Archives: Art

Parity Bitmaps from the OEIS

My friend Alec Jones and I wrote a Python script that takes a two-dimensional sequence in the On-Line Encyclopedia of Integer Sequences and uses it to create a one-bit-per-pixel (1BPP) “parity bitmaps“. The program is simple: it colors a given pixel is black or white depending on whether the corresponding value is even or odd.

A048152 Parity Bitmap
A048152 parity bitmap, rescaled through Lospec’s Pixel Art Scaler.
A207409 parity bitmap
A207409 parity bitmap.

An Unexpected Fractal

We’ve now run the script on over a thousand sequences, but we still both agree on our favorite: the fractal generated by OEIS sequence A279212.

Fill an array by antidiagonals upwards; in the top left cell enter \(a(0)=1\); thereafter, in the \(n\)-th cell, enter the sum of the entries of those earlier cells that can be “seen” from that cell.

Notice that in the images below, increasing the rows and columns by a factor of \(2^n\) seems to increase the “resolution”, because the parity bitmap is self similar at 2x the scale. We still don’t have a good explanation for why we’d expect these images are fractals. If you know, please answer our question about it on Math Stack Exchange. (Alec and I have generated these images up to 16384 × 32768 resolution, roughly 536 megapixels.)

A279212 parity bitmap
512 rows and 256 columns of A279212.
A279212 parity bitmap
2048 rows and 1024 columns of A279212.

The Construction of the Sequence

The sequence is built up by “antidiagonals”, as shown in the GIF below. In the definition, “seen” means every direction a chess queen can move that already has numbers written down (i.e. north, west, northwest, or southwest). That is, look at all of the positions you can move to, add them all up, write that number in your square, move to the next square, and repeat. (The number in cell \(C\) also counts the number of paths a queen can make from \(C\) to the northwest corner using only N, NW, W, SW moves.)

Animation of A279212 construction

(Interestingly, but only tangentially related: Code Golf Stack Exchange User flawr noticed that the number of north/west rook walks is related to the number of ways of partitioning a \(1 \times n\) grid into triangles.)

Parity Bitmaps for Other Sequences

It’s worth noting that many sequences are all black, consist of simple repeating patterns, or look like static. However, chess-type constructions, as illustrated by the GIF above, the one above yield images that look like the Sierpiński triangle. (See A132439 and A334017 below, and look at A334016 and A334745 via their OEIS entries.) Look below for a couple other sequences with interesting images too.

A132439 parity bitmap.
A301851 parity bitmap.
A334017 parity bitmap.
A237620 parity bitmap.

I ordered a poster-sized print of the A279212 fractal for Alec, and he framed it in his office.

Alec’s fractal, framed above his fountain pen ink and tasteful books.

Some ideas for further exploration:

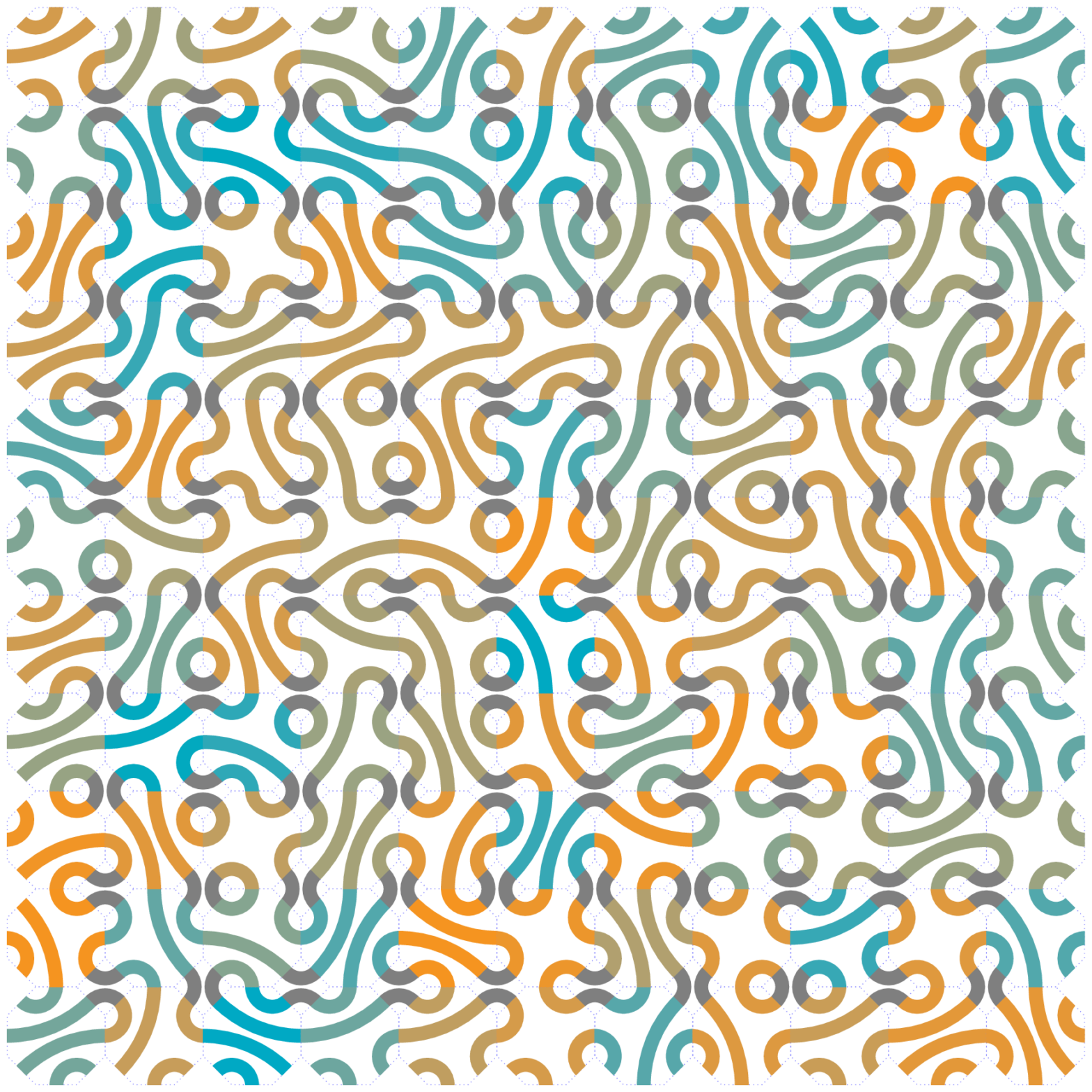
Regular Truchet Tilings

I recently made my first piece of math art for my apartment: a 30″×40″ canvas print based on putting Truchet tiles on the truncated trihexagonal tiling.

A photo of the canvas print
The original image

I first became interested in these sorts of patterns after my former colleague Shane sent me a YouTube video of the one-line Commodore 64 BASIC program:
10 PRINT CHR$(205.5+RND(1)); : GOTO 10

I implemented a version of this program on my website, with the added feature that you could click on a section to recolor the entire component, and this idea was also the basis of Problem 2 and Problem 31 in my Open Problem Collection.

I saw this idea generalized by Colin Beveridge in the article “Too good to be Truchet” in Chalkdust Magazine. In this article, Colin counts the ways of drawing hexagons, octagons, and decagons with curves connecting the midpoints of edges, and regions colored in an alternating fashion. In the case of the hexagon, there are three ways to do it, one of which looks like Palago tiles.

An example of a hexagonal Truchet tiling. Cameron Browne would call this particular example a Palago “creature“, which are counted by Arnauld Chevallier‘s brilliant program.

It turns out that if you ignore the colors, the number of ways to pair up midpoints of the sides of a \(2n\)-gon in such a way that the curves connecting the midpoints don’t overlap is given by the \(n\)-th Catalan number. For example, there are \(C_4 = 14\) ways of connecting midpoints of the sides of an octagon, where different rotations are considered distinct.

Two distinct rotations
Eight distinct rotations
Four distinct rotations

There are three regular tilings of the plane by \(2n\)-gons, the square tiling, the truncated square tiling, and the truncated trihexagonal tiling. Placing a Truchet tile uniformly at random over each of the \(2n\)-gons, results in a really lovely emergent structure.

Square tiling
Truncated square tiling, randomly colored

If you find these designs as lovely as I do, I’d recommend taking a look at the Twitter bots @RandomTiling by Dave Richeson and @Truchet_Nested/@Trichet_Nested by @SerinDelaunay (based on a idea from Christopher Carlson) which feature a series of visually interesting generalizations of Truchet tilings and which are explained in Christopher’s blog post “Multi-scale Truchet Patterns“.

https://twitter.com/Truchet_Nested/status/1363597959011655681

Edward Borlenghi has a blog post “The Curse of Truchet’s Tiles” about how he tried—mostly unsuccessfully—to sell products based on Truchet tiles, like carpet squares and refrigerator magnets (perhaps similar to “YoYo” magnets from Magnetic Poetry). The post is filled with lots of cool, alternative designs for square Truchet tiles and how they fit together. Edward got a patent for some of his ideas, and his attempt to sell these very cool products feels like it could have been my experience in another life.

If you want to see more pretty images and learn more about this, make sure to read Truchet Tilings Revisited by Robert J. Krawczyk! If you want to see what this looks like on a spherical geometry, check out Matt Zucker’s tweet. And if you want to try to draw some of these patterns for yourself, take a look at @Ayliean’s Truchet Tiles Zine.